GATE Civil 2021 Set 2 | GA Question: 9

Question

In the figure shown above, $\text{PQRS}$ is a square. The shaded portion is formed by the intersection of sectors of circles with radius equal to the side of the square and centers at $S$ and $Q$.

The probability that any point picked randomly within the square falls in the shaded area is ____________

• A. $4-\frac{\pi }{2}$
• B. $\frac{1}{2}$
• C. $\frac{\pi }{2}-1$
• D. $\frac{\pi }{4}$

Answer 1

Let the side of the square be $1\;\text{cm},$ then $r = 1\;\text{cm}.$

From the center $S,$ we can draw the circle, and only the quarter part is shown in the figure.

 

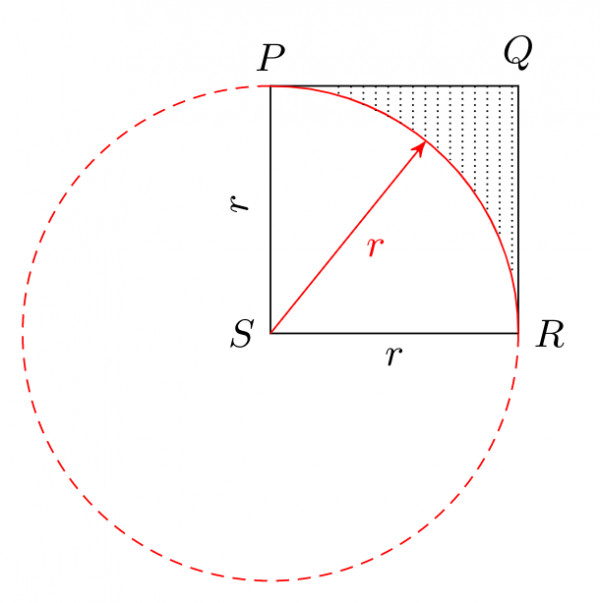
The shaded area $A_{1}  = A_{\text{square}} – A_{\text{quarter circle}} = 1 – \dfrac{\pi}{4}$

From the center $Q,$ we can draw the circle, and only the quarter part is shown in the figure.

 

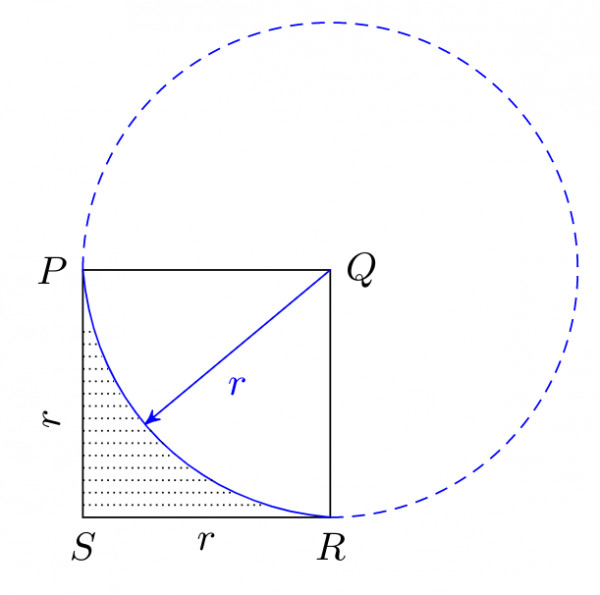
The shaded area $A_{2}  = A_{\text{square}} – A_{\text{quarter circle}} = 1 – \dfrac{\pi}{4}$

Now, we can combine the above two figures, we get,

 

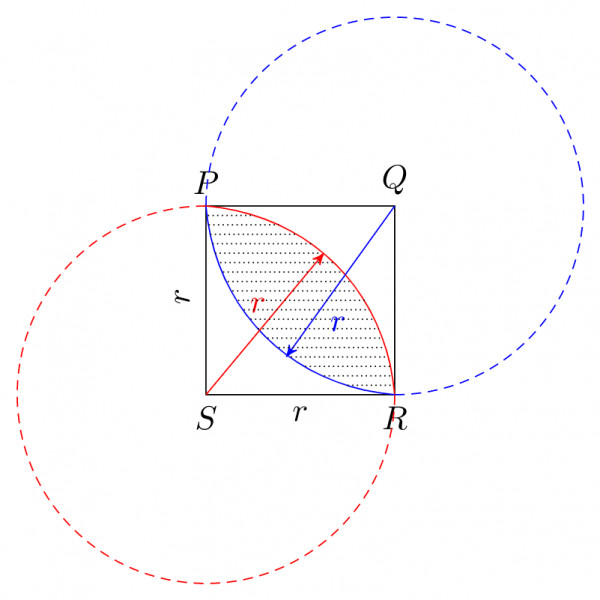
Now, the shaded area $ = A_{\text{square}} – A_{1} – A_{2}$

$\quad = 1 – \left(1-\dfrac{\pi}{4}\right) – \left(1-\dfrac{\pi}{4}\right)$

$\quad = – 1 + \dfrac{2\pi}{4} = \dfrac{\pi}{2} – 1$

Now, the required probability $  = \dfrac{\text{Favorable shaded area}}{\text{Total area}} = \dfrac{\frac{\pi}{2} – 1}{1} = \dfrac{\pi}{2} – 1.$

$\therefore$ The probability that any point picked randomly within the square falls in the shaded area $ = \dfrac{\pi}{2} – 1.$

So, the correct answer is $(C).$