Given the bar graph.
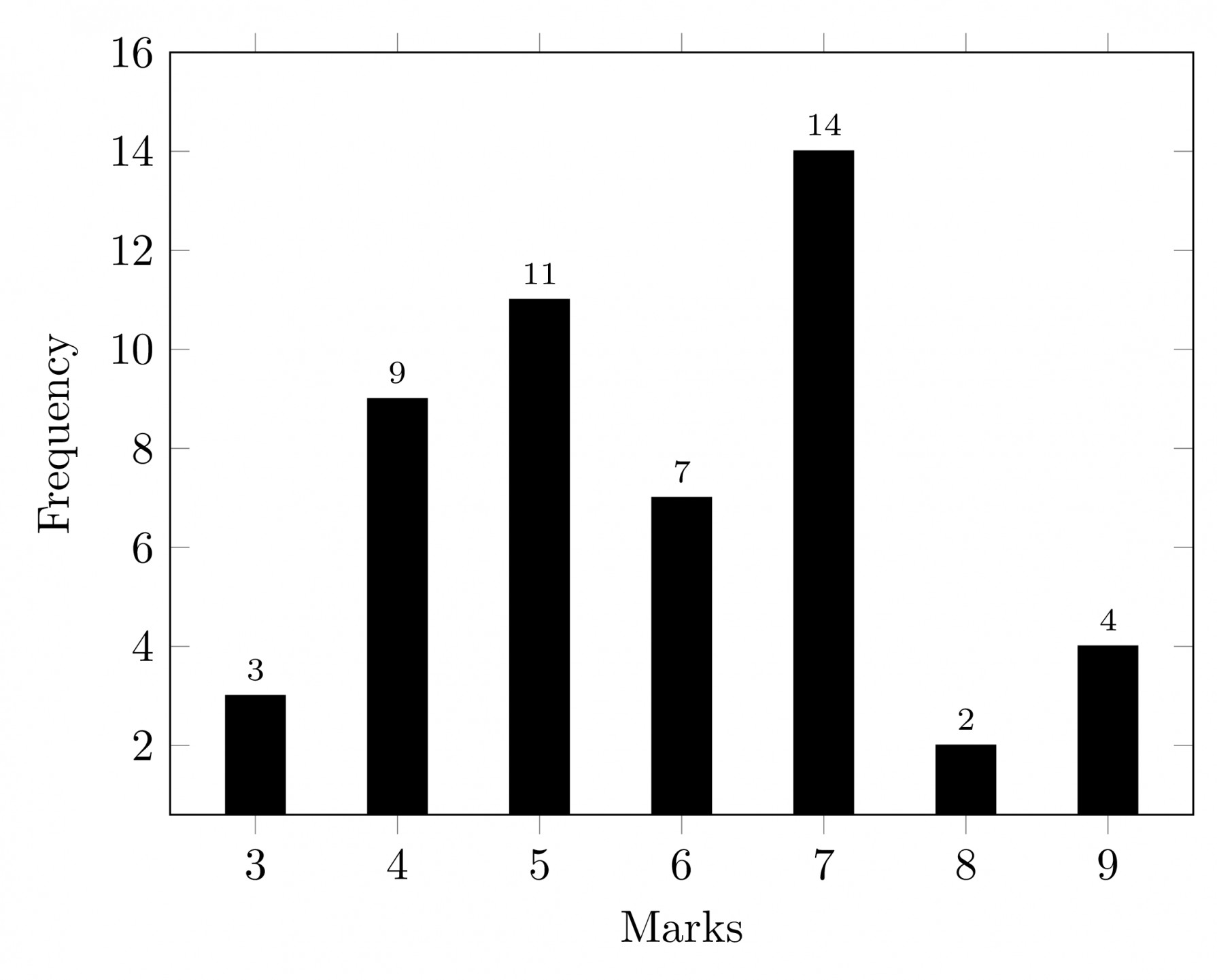
Total marks, $N = 3+9+11+7+14+2+4 = 50\;{\color{Red}{\text{(even)}}}$
${\color{Blue}{\textbf{Mean:}}}$ Suppose $x_{1}, x_{2}, x_{3},\dots , x_{n}$ be $n$ observations with respective frequencies $f_{1}, f_{2}, f_{3},\dots, f_{n}.$ This means, the observation $x_{1}$ occurs $f_{1}$ times, $x_{2}$ occurs $f_{2}$ times, $x_{3}$ occurs $f_{3}$ times and so on.
$\Rightarrow \boxed{\overline{x} = \dfrac{f_{1}x_{1} + f_{2}x_{2} + f_{3}x_{3} + \dots + f_{n}x_{n} }{f_{1} + f_{2} + f_{3} + \dots + f_{n}}}$
$\Rightarrow \boxed{\overline{x} = \displaystyle{} \dfrac{\displaystyle{}\sum_{i=1}^{n}f_{i}x_{i}}{\displaystyle{}\sum_{i=1}^{n}f_{i}}}$
Now, $\overline{x} = \dfrac{3 \times 3 + 9 \times 4 + 11 \times 5 + 7 \times 6 + 14 \times 7 + 2 \times 8 + 4 \times 9}{3+9+11+7+14+2+4}$
$\Rightarrow \overline{x} = \dfrac{9 + 36 + 55 + 42 + 98 + 16 + 36}{50} = \dfrac{292}{50}$
$\Rightarrow {\color{Blue}{\boxed{\overline{x} = 5.84}}}$
${\color{Magenta}{\textbf{Mode:}}}$ Mode is which observation in a frequency distribution that occurs the maximum times in the frequency distribution, or technically speaking, which has the highest frequency.
$${\color{Green}{\boxed{\text{Mode = 3 Median – 2 Mean}}}}$$
So, ${\color{Magenta}{\boxed{\text{mode} = 7}}}$
Now, $7 = 3\; \text{Median – 2 (5.84)}$
$\Rightarrow 3\; \text{Median} = 7 + 11.68$
$\Rightarrow 3\; \text{Median} = 18.68$
$\Rightarrow {\color{Purple}{ \boxed{\text{Median} = 6.22}}}$
$\therefore {\color{DarkBlue}{\boxed{\text{mode > median> mean} = 7 > 6.22>5.84}}}$
Correct Answer $:\text{B}$
$\textbf{PS:}$
${\color{Purple}{\textbf{Median:}}}$ A median is a measure of central tendency which divides data into $2$ parts, separating the upper and lower half of the data by a value which is called the median value.
Arrange all the observations in an ascending order. See whether the number of observations is an odd or even number. If the number is odd, use the formula $$\left(\dfrac{N+1}{2}\right)^{\text{th}}$$ observation, where $N$ is the number of observations.$$\textbf{(Or)}$$
$$\text{Median}=\left(\dfrac{N+1}{2}\right)^{\text{th}}\text{term}$$When the number of observations are even, the median is calculated by taking the average of the $$\left(\dfrac{N}{2}\right)^{\text{th}}$$ observation and the next observation. $$\textbf{(Or)}$$
$$\text{Median}=\dfrac{\left(\dfrac{N}{2}\right)^{\text{th}}\text{term}+\left(\dfrac{N}{2}+1\right)^{\text{th}}\text{term}}{2}$$