Let the side of the square $\square \text{SPQT and } \square\text{RUVZ}$ be $a\;\text{cm and }b\;\text{cm}$ respectively.
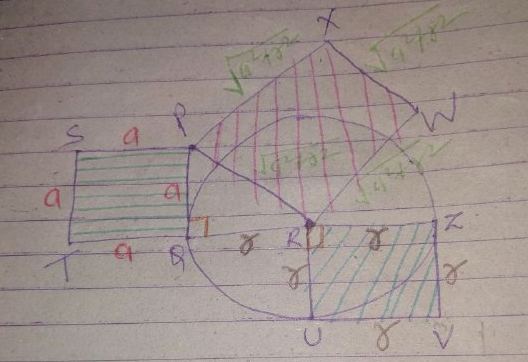
The triangle $\triangle \text{PQR}$ is a right-angle triangle. So we can apply the Pythagorean theorem.
${\color{Green}{\boxed{\text{(Hypotenuse)}^{2} = \text{(Perpendicular)}^{2} + \text{(Base)}^{2}}}}$
$\Rightarrow (\text{PR})^{2} = (\text{PQ})^{2} + (\text{QR})^{2}$
$\Rightarrow (\text{PR})^{2} = a^{2} + r^{2}$
$\Rightarrow \boxed{\text{PR} = \sqrt{a^{2} + r^{2}}}$
Now, we can easily calculate the area of the squares, $\square \text{PXWR}, \square \text{RUVZ} \;\text{and}\; \square \text{SPQT}:$
- Area of $\square \text{SPQT} = a^{2}\;\text{cm}^{2}$
- Area of $\square \text{RUVZ} = r^{2}\;\text{cm}^{2}$
- Area of $\square \text{PXWR} = (a^{2} + r^{2})\;\text{cm}^{2}$
We can clearly see, $\text{Area of}\; \square \text{PXWR = Area of}\; \square \text{SPQT + Area of}\; \square \text{RUVZ}$
$\Rightarrow {\color{Blue}{\boxed{\text{Area of}\; \square \text{SPQT = Area of}\; \square \text{PXWR - Area of}\; \square \text{RUVZ}}}}$
Correct Answer $:\text{B}$