Let’s first draw the diagram.
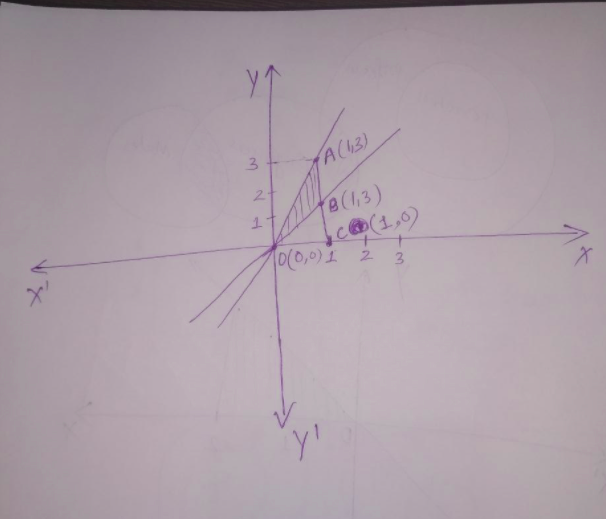
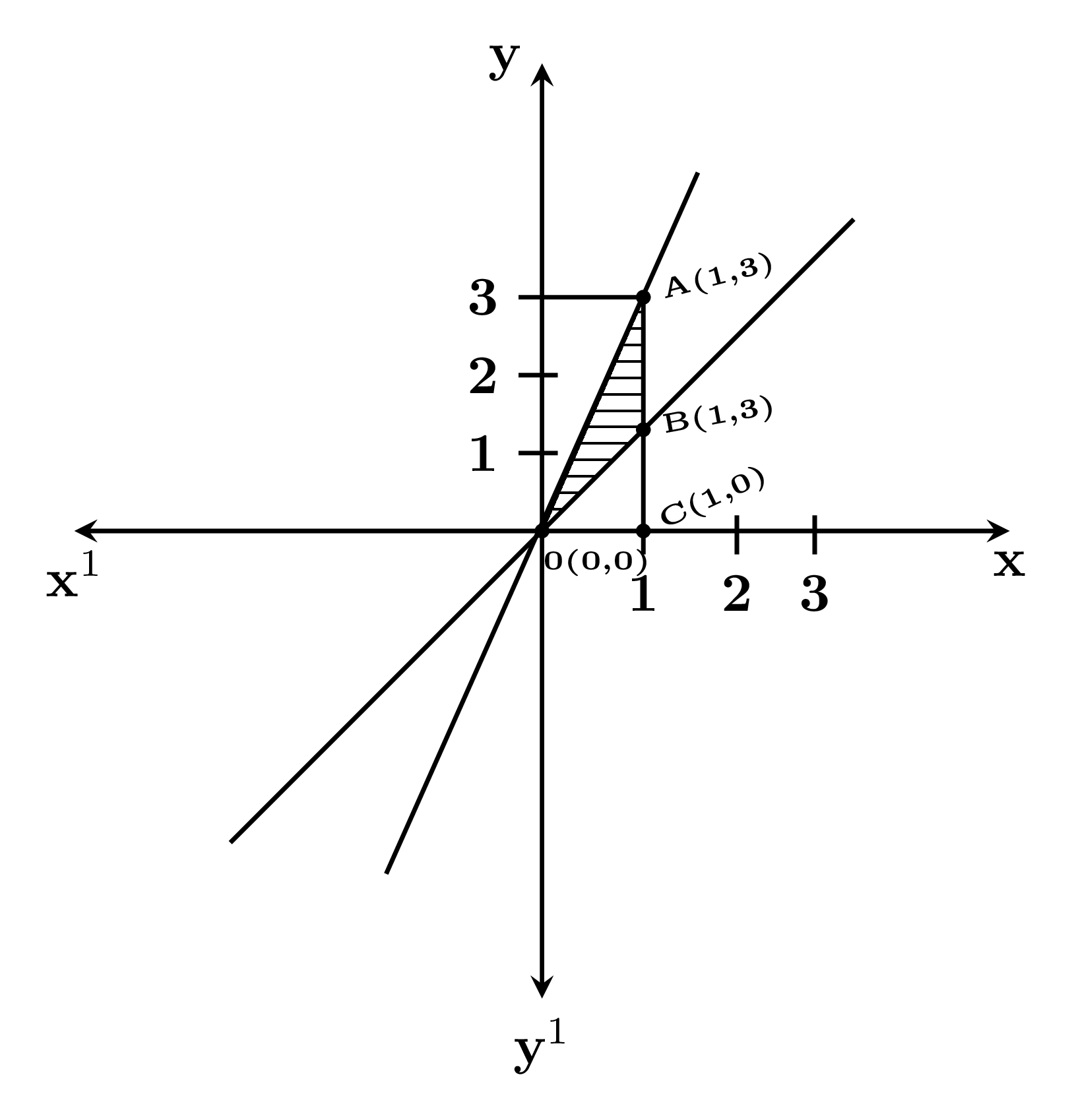
The area enclosed between the straight lines in the interval $[0,1]$ on the $x$-axis $ = \text{area of}\;\triangle \text{ACO} – \text{area of}\;\triangle \text{BCO}$
$= \dfrac{1}{2} \times 1 \times 3\; – \dfrac{1}{2} \times 1 \times 2 = \dfrac{1}{2}(3-2) = \dfrac{1}{2} = 0.5\;\text{unit}^{2}.$
Correct Answer $:\text{A}$
$\textbf{PS:}$ The area of triangle ${\color{Green}{ = \dfrac{1}{2} \times \text{Base} \times \text{Height}}}$