The concentrations $s(x,t)$ of pollutants in a one-dimensional reservoir at position $x$ and time $t$ satisfies the diffusion equation
$$\frac{\partial s (x,t)}{\partial t} = D \frac{\partial^{2}s (x,t)}{\partial x^{2}}$$
on the domain $0 \leq x \leq L,$ where $D$ is the diffusion coefficient of the pollutants. The initial condition $s(x,0)$ is defined by the step-function shown in the figure.
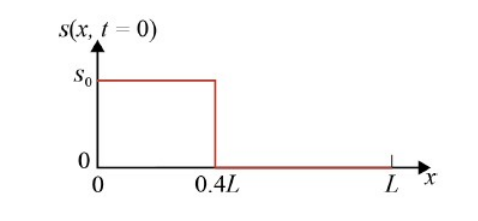
The boundary conditions of the problems of the problem are given by $\frac {\partial s (x,t)}{\partial x} = 0$ at the boundary points $x = 0$ and $x = L$ at all times. Consider $D = 0.1 \; \text{m}^{2} \text{/s,} \; s_{0} = 5 \; \mu \text{mol/m},$ and $L = 10 \; \text{m.}$
The steady-state concentration $\widetilde{s} \left( \dfrac{L}{2} \right) = s \left(\dfrac{L}{2}, \infty \right)$ at the center $x=\dfrac{L}{2}$ of the reservoir (in $\mu \text{mol/m}$) is ______________. (in integer)