Consider two linear elastic rods $HI$ and $IJ$, each of length $b$, as shown in the figure. The rods are co-linear, and confined between two fixed supports at $H$ and $J.$ Both the rods are initially stress free. The coefficient of linear thermal expansion is $\alpha$ for both the rods. The temperature of the rod $IJ$ is raised by $\Delta T,$ whereas the temperature of rod $HI$ remains unchanged. An external horizontal force $P$ is now applied at node $I.$ It is given that $\alpha = 10^{-6}\; ^{\circ} \text{C}^{-1}, \Delta T = 50 \; ^{\circ} \text{C}, b=2 \; \text{m}, AE = 10^{6} \; \text{N}.$ The axial rigidities of the rods $HI$ and $IJ$ are $2AE$ and $AE,$ respectively.
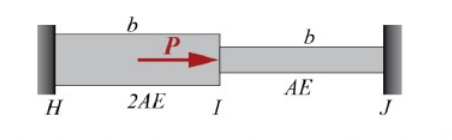
To make the axial force in rod $HI$ equal to zero, the value of the external force $P$ (in $\text{N}$) is ____________ . (round off to the nearest integer)