Given that,
- $n(\text{U}) = 450$
- $n(\text{M}) = 150$
- $n(\text{P}) = 200$
- $n(\text{C}) = 175$
- $n(\text{M} \cap \text{P}) = 50$
- $n(\text{P} \cap \text{C}) = 60$
- $n(\text{M} \cap \text{C}) = 40$
- $n(\text{M} \cap \text{P} \cap \text{C}) = 30$
- ${\color{Red}{n(\text{H}) = \;?}}$
Let’s draw the Venn diagram.
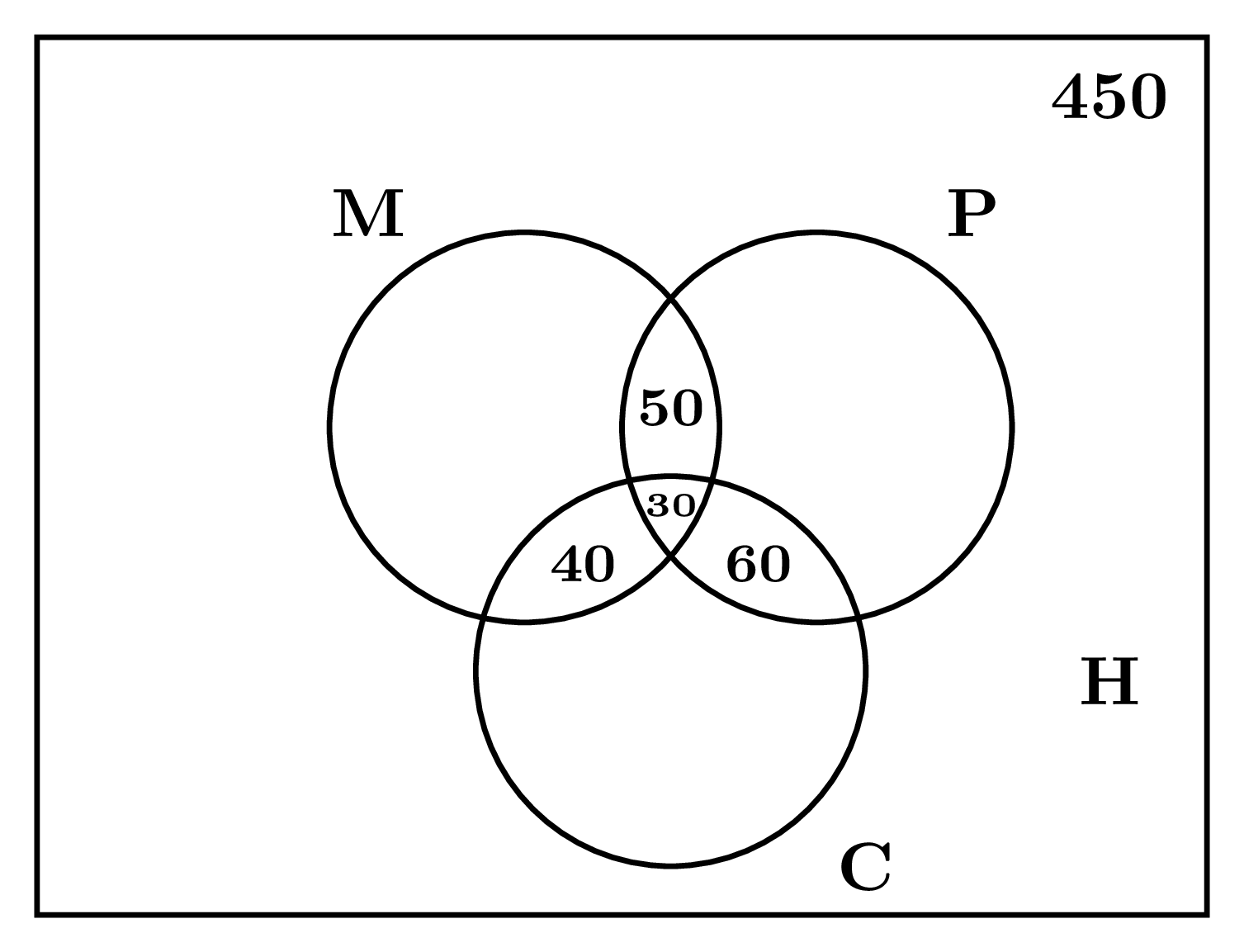
Now, $n(\text{M} \cup \text{P} \cup \text{C}) = n(\text{U}) + n(\text{M}) + n(\text{P}) – n(\text{C}) – n(\text{M} \cap \text{P}) – n(\text{P} \cap \text{C}) - n(\text{M} \cap \text{C}) + n(\text{M} \cap \text{P} \cap \text{C})$
$\Rightarrow n(\text{M} \cup \text{P} \cup \text{C}) = 150+200+175-50-60-40+30 = 555-150 = 405$
Now, $n(\text{U}) = n(\text{M} \cup \text{P} \cup \text{C}) + n(\text{H})$
$\Rightarrow n(\text{H}) = 450-405$
$\Rightarrow {\color{Blue}{\boxed{n(\text{H}) = 45}}}$
$\therefore$ The number of students interested in Humanities is $45.$
Correct Answer $:\text{D}$