Given that,
- $2x – 3y = 5 \quad \longrightarrow (1)$
- $3x + 2y = 8 \quad \longrightarrow (2)$
- $4x – 6y = 5 \quad \longrightarrow (3)$
- $6x – 9y = 6 \quad \longrightarrow (4)$
From equation $(1),$
$2x – 3y = 5$
$\Rightarrow -3y = -2x + 5$
$\Rightarrow y = \frac{2}{3}x – \frac{5}{3}$
Slope of the line, ${\color{Blue}{\boxed{m_{1} = \frac{2}{3}}}}$
From equation $(2),$
$3x + 2y = 8$
$\Rightarrow 2y = -3x + 8$
$\Rightarrow y = \frac{-3}{2}x + 4$
Slope of the line, ${\color{Purple}{\boxed{m_{2} = \frac{-3}{2}}}}$
From equation $(3),$
$4x – 6y = 5$
$\Rightarrow -6y = -4x + 5$
$\Rightarrow y = \frac{2}{3}x - \frac{5}{6}$
Slope of the line, ${\color{DarkOrange}{\boxed{m_{3} = \frac{2}{3}}}}$
From equation $(4),$
$6x – 9y = 6$
$\Rightarrow -9y = -6x + 6$
$\Rightarrow y = \frac{2}{3}x – \frac{2}{3}$
Slope of the line, ${\color{Teal}{\boxed{m_{4} = \frac{2}{3}}}}$
We get, ${\color{Red}{\boxed{m_{1} = m_{3} = m_{4} = \frac{2}{3}}}}$
The lines $\text{L1, L3, and L4}$ are parallel to each other.
Now,
- $m_{1} \times m_{2} = \frac{2}{3} \times \frac{-3}{2} = -1$
- $m_{3} \times m_{2} = \frac{2}{3} \times \frac{-3}{2} = -1$
- $m_{4} \times m_{2} = \frac{2}{3} \times \frac{-3}{2} = -1$
The lines $\text{L1, L3, and L4}$ are perpendicular to $\text{L2}.$
${\color{Magenta}{\textbf{Second Method:}}}$
The line $\text{L1}: y = \frac{2}{3}x – \frac{5}{3}$
Slope of the line, ${\color{Blue}{\boxed{m_{1} = \frac{dy}{dx} = \frac{2}{3}}}}$
The line $\text{L2}: y = \frac{-3}{2}x + 4$
Slope of the line, ${\color{Purple}{\boxed{m_{2} = \frac{dy}{dx} = \frac{-3}{2}}}}$
The line $\text{L3}: y = \frac{2}{3}x - \frac{5}{6}$
Slope of the line, ${\color{DarkOrange}{\boxed{m_{3} = \frac{dy}{dx} = \frac{2}{3}}}}$
The line $\text{L4}:y = \frac{2}{3}x – \frac{2}{3}$
Slope of the line, ${\color{Teal}{\boxed{m_{4} = \frac{dy}{dx} = \frac{2}{3}}}}$
Correct Answer $:\text{D}$
${\color{Red}{\textbf{PS:}}}$ The general form of line given by $y = mx + c;$ where $m$ is the slope and $c$ is the intercept on $y$-axis.
${\color{Lime}{\textbf{Parallel lines:}}}$ Parallel lines are lines that do not meet at any point in the $xy$-plane. Another way to characterize parallel lines are distinct lines with the same slope. Suppose we are given two non-vertical lines in slope-intercept form:
$$\begin{aligned} y &= m_1 x + b_1\\ y &= m_2 x + b_2. \end{aligned}$$
$\text{The two lines are parallel if} \; {\color{Purple}{\boxed{m_1 = m_2, \;\text{and}\; b_1 \ne b_2.}}}$
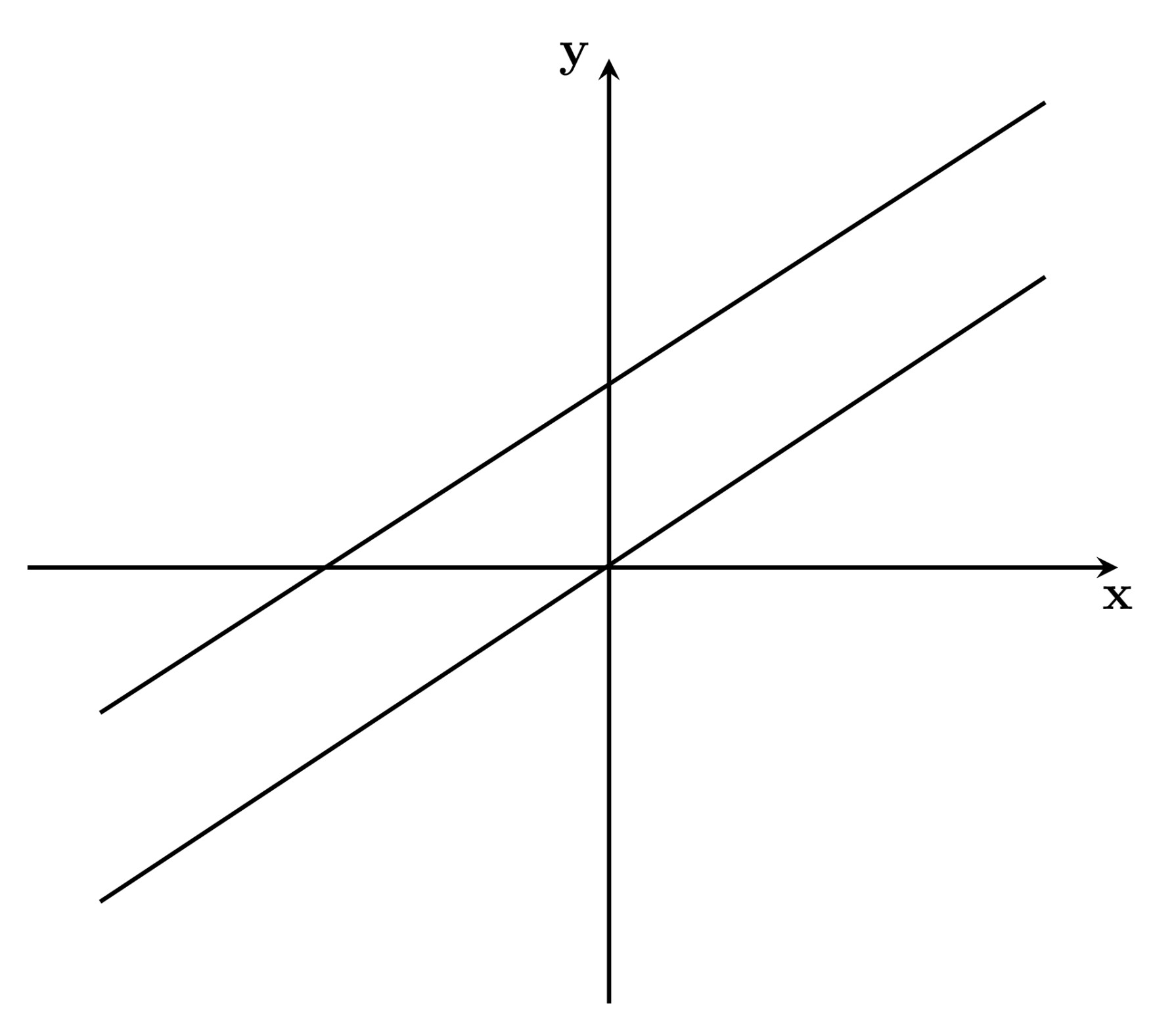
${\color{Olive}{\textbf{Perpendicular Lines:}}}$ A pair of lines is perpendicular if the lines meet at $90^\circ$ angle. Given two non-vertical lines in slope-intercept form
$$\begin{aligned} y &= m_1 x + b_1\\ y &= m_2 x + b_2, \end{aligned}$$
The two lines are perpendicular if ${\color{Teal}{\boxed{m_1 = - \frac{1}{m_2} \Rightarrow m_{1} \times m_{2} = -1}}}$, that is, if the slopes are negative reciprocals of each other.

${\color{Magenta}{\textbf{Finding slope using differentiation:}}}$ For a line of the form (or any other form) $y=mx+c,$ we can find its slope by simply taking any two values of $x, {x}_{1}$ and ${x}_{2},$ and their respective $y$ values, ${y}_{1}$ and ${y}_{2}$. We find the slope by the formula $\tan \theta =\dfrac {{y}_{1}-{y}_{2}}{{x}_{1}- {x}_{2}}$. In the case of curves our approach is somewhat different. In the above case, we had $\Delta y={y}_{1}-{y}_{2}$ and $\Delta x={x}_{1}-{x}_{2}$. Now we need to find the slope of tangent to a curve at some point. To do this we again need
$$\tan \theta =\frac {{y}_{1}-{y}_{2}}{{x}_{1}- {x}_{2}},$$
but this time $\Delta y$ and $\Delta x$ tend to zero, which means the interval is very small because it is a tangent at a point.
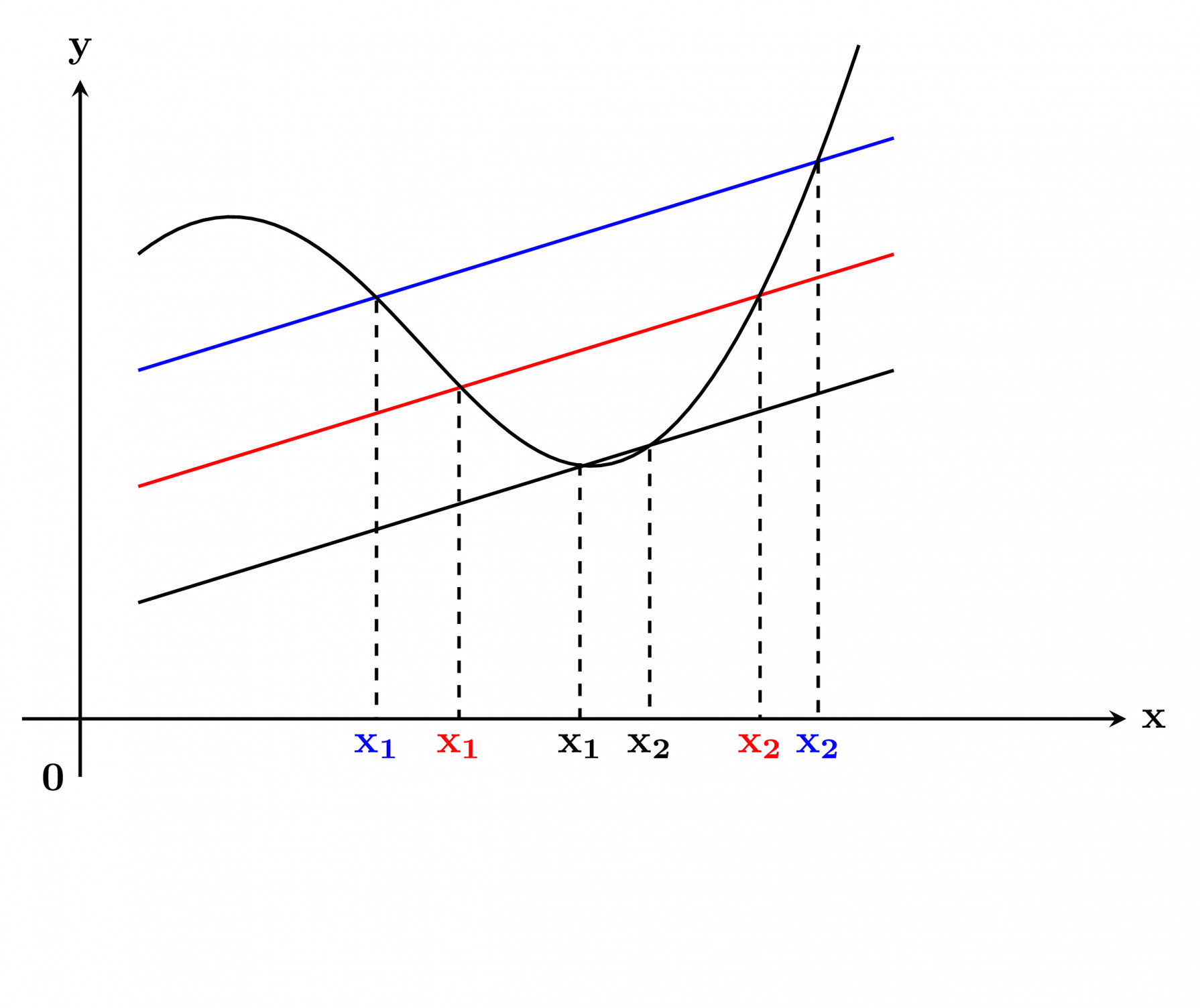
Notice that as the colored pairs of $x_1$ and $x_2$ come closer, the tangent shifts to a point on the graph.
When this happens we replace
$$\frac { \Delta y }{ \Delta x } \quad \text{by}\quad \frac { dy }{ dx }$$