The relationship between oxygen consumption and equivalent biodegradable organic removal (i.e.,BOD) in a closed container with respect to time is shown in the figure
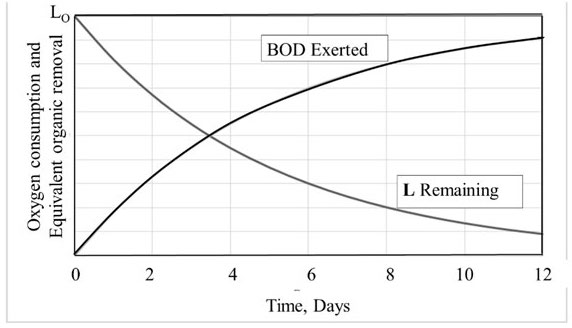
Assume that the rate of oxygen consumption is directly proportional to the amount of degradable organic matter and is expressed as $\large\frac{dL_t}{dt} = -kL_t$, where, $L_t\: (\text{in mg/litre})$ is the oxygen equivalent of the organics remaining at time $t$ and $k \:(\text{in}\: d^{-1})$is the degradation rate constant. $L_0$ is the oxygen equivalent of organic matter at time, $t=0$.
In the above context,the correct expression is
- $BOD_5 = L_5$
- $BOD_t = L_0-L_t$
- $L_0 = L_te^{-kt}$
- $L_t = L_0(1-e^{-kt})$