GATE Civil 2022 Set 1 | GA | Question: 9

Question

In the square grid shown on the left, a person standing at $\text{P2}$ position is required to move to $\text{P5}$ position.

The only movement allowed for a step involves, “two moves along one direction followed by one move in a perpendicular direction”. The permissible directions for movement are shown as dotted arrows in the right.

For example, a person at a given position $\text{Y}$ can move only to the positions marked $\text{X}$ on the right.

Without occupying any of the shaded squares at the end of each step, the minimum number of steps required to go from $\text{P2}$ to $\text{P5}$ is

• A. $4$
• B. $5$
• C. $6$
• D. $7$

Comments

pro tip:if you are not properly read the question then our mind says that we cant go through shaded squares but actual thing is we can go but last step cant be in the shaded square.

---

I did this mistake and spent lot of time :\

---

so do I..

---

damn, did the same mistake

Answer 1

Using the above information given in the question, we can move a person from $\text{P2 to P5.}$

A person can move from $\text{P2 to P5}$ in the following way (minimum number of steps):

• ${\color{Blue}{\text{P2} \overset{1}{\longrightarrow} \text{Q4} \overset{2}{\longrightarrow} \text{S3} \overset{3}{\longrightarrow} \text{Q2} \overset{4}{\longrightarrow} \text{R4} \overset{5}{\longrightarrow} \text{P5}}}$

Another way is also possible, with the minimum number of steps.

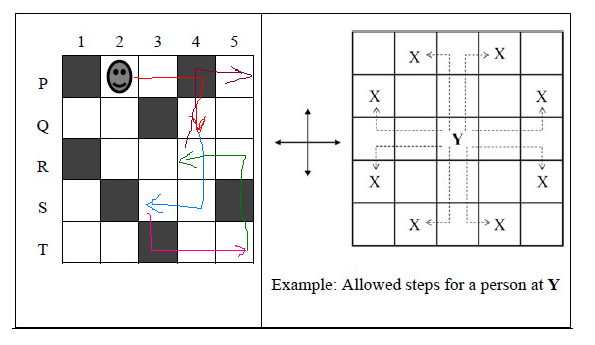
A person can move from $\text{P2 to P5}$ in the following way (minimum number of steps):

• ${\color{Purple}{\text{P2} \overset{1}{\longrightarrow} \text{Q4} \overset{2}{\longrightarrow} \text{S3} \overset{3}{\longrightarrow} \text{T5} \overset{4}{\longrightarrow} \text{R4} \overset{5}{\longrightarrow} \text{P5}}}$

$\therefore$ The minimum number of steps required (for a person) to go from $\text{P2 to P5}$ is $5.$

Correct Answer $:\text{B}$

Comments

a little bit of modification is req in the fig I guess.
cuz the initial step was incorrect.

 

---

@Ghost Riley 

go $2$ steps forward first and then go $1$ step left/right or go $1$ step left/right first and then go $2$ steps forward is same. you will reach at same place.

---

@Lakshman Bhaiya nice solution.

---

here how you can go to s3 to t5 in questions saying that first two steps and perpendicularly one step u r doing first perpendicularly and then moving 2 steps is it possible?

Answer 2

Easier if we backtrack from P5. R4 is the only block that can be used to reach P5. R4 can be reached through T5 or Q2. T5 seems too far so will choose Q2 for now and backtrack if necessary and choose Following similar procedure we can conclude that no path with less than 5 steps is possible.

Answer 3

One more way can be:

P2 --> R3 --> S1 --> Q2 --> R4 --> P5

Answer 4

5 Steps

Answer 5

Here is solution