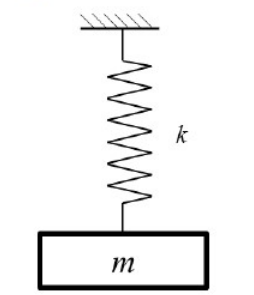
An undamped spring-mass system with mass $m$ and spring stiffness $k$ is shown in the figure. The natural frequency and natural period of this system are $\omega \; \text{rad/s}$ and $T \; \text{s},$ respectively. If the stiffness of the spring is doubled and the mass is halved, then the natural frequency and the natural period of the modified system, respectively, are
- $2 \omega \; \text{rad/s}$ and $T/2 \; \text{s}$
- $\omega/2 \; \text{rad/s}$ and $2T \; \text{s}$
- $4 \omega \; \text{rad/s}$ and $T/4 \; \text{s}$
- $ \omega \; \text{rad/s}$ and $T \; \text{s}$