A plate in equilibrium is subjected to uniform stresses along its edges with magnitude $\sigma_{xx} = 30 MPa$ and $\sigma_{yy} = 50 MPa$ as shown in the figure.
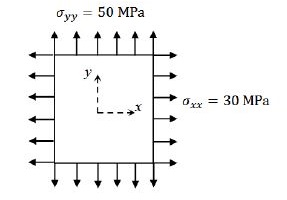
The Young's modulus of the material is $2 \times 10^{11} \: N/m^2$ and the Poisson's ratio is $0.3$. If $\sigma_{zz}$ is negligibly small and assumed to be zero, then the strain $\varepsilon_{zz}$
- $-120 \times 10^{-6}$
- $-60 \times 10^{-6}$
- $0.0$
- $120 \times 10^{-6}$